Théorie de la réaction – machine synchrone saillante

Théorie de deux réactions a été proposé par Andre Blondel. La théorie propose de résoudre les MMF en armature donnés en deux composants mutuellement perpendiculaires, avec un le long de l’axe du rotor du pôle saillant. Il est connu comme le axe direct ou axe d composant. L’autre composant est situé perpendiculaire à l’axe du poteau saillant du rotor. Il est connu comme le axe quadrature ou axe Q composant.

Le composant de l’axe d du mmf d’armature, f_un est indiqué par f_d, et la composante de l’axe Q par f_q. Le composant f_d est de magnétisation ou de démagnétisation. Le composant f_q se traduit par un effet croisé. Si ψ est l’angle entre le courant d’armature i_un et la tension d’excitation e_f et f_un est l’amplitude du MMF d’armature, alors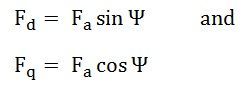

Machine synchrone à pôle saillant deux théorie de la rection

Dans la machine synchrone du rotor cylindrique, l’espace d’air est uniforme. La structure du poteau du rotor d’une machine à poteaux saillants rend l’espace d’air très non uniforme. Considérons un rotor de poteau à 2 pôles et saillant tournant dans le sens antihoraire dans un stator à 2 pôles comme indiqué sur la figure ci-dessous:

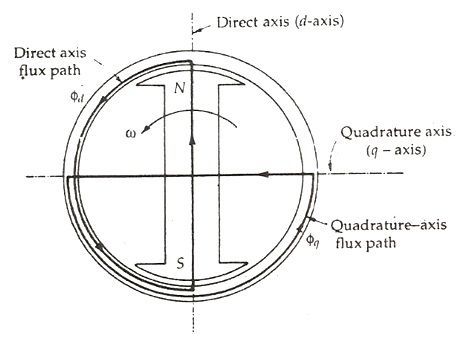L’axe le long de l’axe du rotor est appelé l’axe direct ou D. L’axe perpendiculaire à l’axe D est connu sous le nom de quadrature ou axe Q. Le chemin de flux de l’axe direct implique deux petits espaces d’air et est le chemin de la réticence minimale. Le chemin illustré dans la figure ci-dessus par ϕ_q A deux grandes lacunes d’air et est le chemin de la réticence maximale.

Le flux de rotor b_R est montré verticalement vers le haut comme indiqué dans la figure ci-dessous:

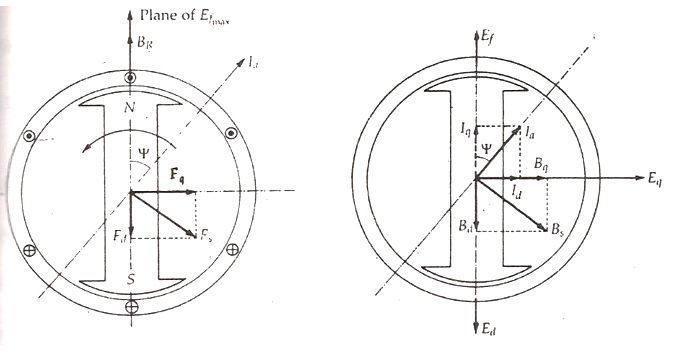Le flux de rotor induit une tension e_f dans le stator. Le courant d’armature du stator i_un Va circuler dans le moteur synchrone lorsqu’une charge de facteur de puissance en retard y est connectée. Ce courant d’armature stator i_un est en retard sur la tension générée E_f par un angle ψ.

Le courant d’inhabituel produit la force magnétomotive du stator f_s. Ce MMF est en retard de moi_un par angle de 90 degrés. Le MMF F_S produit le champ magnétique du stator b_S long la direction de FS. Le stator MMF est résolu en deux composants, à savoir le composant de l’axe direct F_d et le composant de l’axe quadrature F_q.

Si,

• ϕ_d est le flux de l’axe direct
• Φ_q est le flux de l’axe quadrature
• R_d est la réticence du chemin de flux de l’axe direct

Donc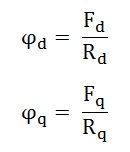

Comme, r_d qle composant de l’axe direct de MMF F_d produit plus de flux que le composant de l’axe quadrature du MMF. Les flux de l’axe direct et en quadrature produisent une tension dans les enroulements du stator par réaction d’armature.

Laisser,

• E_annonce être le composant de l’axe direct de la tension de réaction de l’armature.
• E_aq être le composant de l’axe quadrature de la tension de réaction de l’armature.

Étant donné que chaque tension de réaction d’armature est directement proportionnelle à son courant de stator et est en retard par des angles de 90 degrés. Par conséquent, les tensions de réaction d’armature peuvent être écrites comme indiqué ci-dessous: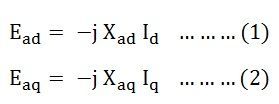

Où,

• X_annonce est la réactance de réaction d’armature dans l’axe direct par phase.
• X_aq est la réactance de réaction d’armature dans l’axe quadrature par phase.

La valeur de x_annonce est toujours plus grand que x_aq. Comme l’EMF induit par un MMF donné agissant sur l’axe direct est plus petit que pour l’axe en quadrature en raison de sa réticence plus élevée.

La tension totale induite dans le stator est la somme d’EMF induite par l’excitation de champ. Les équations sont écrites comme suit: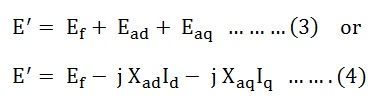

La tension e ‘est égale à la somme de la tension du borne V et des chutes de tension dans la résistance et la réactance des fuites de l’armature. L’équation est écrite comme: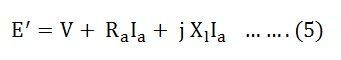

Le courant d’armature est divisé en deux composants; L’un est la phase avec la tension d’excitation E_f et l’autre est en quadrature de phase.

Si

• je_q est la composante de l’axe de i_un en phase avec e_f.
• je_d est l’axe d i_un En retard E_f par 90 degrés.

Donc,

Combinant l’équation (4) et (5) nous obtenons,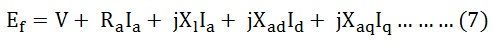

Combinant l’équation (6) et (7) nous obtenons,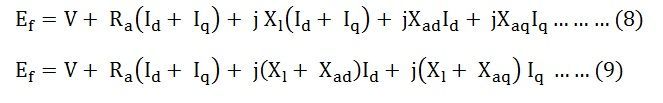 Laisser,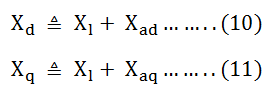

La réactance X_d est appelé le réactance synchrone de l’axe directet la réactance X_q est appelé le Réactance synchrone de l’axe quadrature.

En combinant les équations (9) (10) et (11), nous obtenons les équations ci-dessous: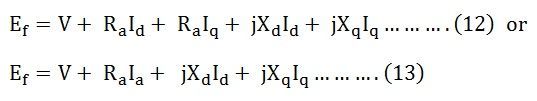 L’équation (12) illustrée ci-dessus est l’équation de tension finale pour un générateur synchrone saillant.