Théorème de superposition

Théorème de superposition déclare que dans tout réseau bilatéral linéaire, actif et ayant plus d’une source, la réponse à travers n’importe quel élément est la somme des réponses obtenues à partir de chaque source considérée séparément et toutes les autres sources sont remplacées par leur résistance interne. Le théorème de superposition est utilisé pour résoudre le réseau où deux sources ou plus sont présentes et connectées.

Contenu:

• Explication du théorème de superposition
• Étapes pour résoudre le réseau par le théorème de superposition
• Vidéo

En d’autres termes, il peut être indiqué comme si un certain nombre de sources de tension ou de courant agissent dans un réseau linéaire, le courant résultant dans n’importe quelle branche est la somme algébrique de tous les courants qui y seraient produits lorsque chaque source agit seule pendant que Toutes les autres sources indépendantes sont remplacées par leurs résistances internes.

Il ne s’applique qu’au circuit qui est valable pour la loi de l’Ohm (c’est-à-dire pour le circuit linéaire).

Explication du théorème de superposition

Comprenons le théorème de superposition à l’aide d’un exemple. Le diagramme du circuit est illustré ci-dessous se compose de deux sources de tension V₁ et V₂.

Tout d’abord, prenez la source V₁ seul et court-circuit le V₂ Source comme indiqué dans le diagramme du circuit ci-dessous:

Ici, la valeur du courant coulant dans chaque branche, c’est-à-dire i₁‘, je₂‘Et je₃«est calculé par les équations suivantes.

La différence entre les deux équations ci-dessus donne la valeur de l’i3 actuel ‘

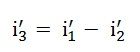
Maintenant, activant la source de tension V₂ et désactiver la source de tension V₁ En le circuisant, trouvez les différents courants, c’est-à-dire i₁ », je₂ », je₃ » coulant dans le diagramme du circuit illustré ci-dessous:

Ici,

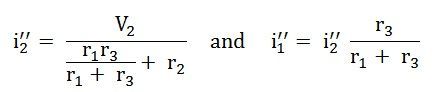
Et la valeur du actuel i₃ » sera calculé par l’équation ci-dessous:

Selon le théorème de superposition, la valeur du courant i₁je₂je₃ est maintenant calculé comme:

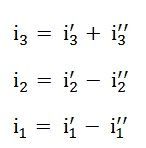
La direction du courant doit être prise en charge tout en trouvant le courant dans les différentes branches.

Étapes pour résoudre le réseau par le théorème de superposition

Compte tenu du diagramme du circuit A, voyons les différentes étapes pour résoudre le théorème de superposition:

Étape 1 – Prenez une seule source indépendante de tension ou de courant et désactiver les autres sources.

Étape 2 – Dans le diagramme du circuit b indiqué ci-dessus, considérez la source e₁ et remplacer l’autre source e₂ par sa résistance interne. Si sa résistance interne n’est pas donnée, elle est considérée comme zéro et que la source est court-circuitée.

Étape 3 – S’il y a une source de tension que le court-circuit et s’il y a une source de courant, ouvrez-le.

Étape 4 – Ainsi, en activant une source et en désactivant l’autre source, trouvez le courant dans chaque branche du réseau. Prenant l’exemple ci-dessus, trouvez le actuel i₁‘, JE₂‘Et je₃‘.

Étape 5 – Considérez maintenant l’autre source e₂ et remplacer la source e₁ par sa résistance interne r₁ comme indiqué dans le diagramme du circuit C.

Étape 6 – Déterminer le courant dans diverses sections, i₁ », JE₂ » Et moi₃ ».

Étape 7 – Maintenant, pour déterminer le courant de branche net en utilisant le théorème de superposition, ajoutez les courants obtenus de chaque source individuelle pour chaque branche.

Étape 8 – Si le courant obtenu par chaque branche est dans la même direction, ajoutez-les et s’il est dans le sens opposé, soustrayez-les pour obtenir le courant net dans chaque branche.

Le flux réel de courant dans le circuit C sera donné par les équations ci-dessous:

Vidéo: Théorème de superposition

Ainsi, de cette manière, nous pouvons résoudre le théorème de superposition.