Le Théorème de Millman indique que – lorsque un certain nombre de sources de tension (V1V2V3……… Vn) sont en parallèle ayant une résistance interne (R1R2R3………… .rn) respectivement, l’arrangement peut remplacer par une seule source de tension équivalente V en série par une résistance de série équivalente R. En d’autres termes; Il détermine la tension à travers les branches parallèles du circuit, qui ont plusieurs sources de tension, c’est-à-dire réduit la complexité du circuit électrique.
Contenu:
- Explication du théorème de Millman
- Étapes pour résoudre le théorème de Millman
Ce théorème est donné par Jacob Millman. L’utilité de Théorème de Millman est que le nombre de sources de tension parallèle peut être réduite à une source équivalente. Il est applicable uniquement à résoudre la branche parallèle avec une résistance connectée à une source de tension ou une source de courant. Il est également utilisé dans la résolution du réseau ayant un circuit de pont déséquilibré.
 Selon le théorème de Millman
Selon le théorème de Millman
Explication du théorème de Millman
En supposant un réseau CC de nombreuses sources de tension parallèle avec des résistances internes fournissant une puissance à une résistance de charge RL comme indiqué sur la figure ci-dessous
 Laissez-je représenter le courant résultant des sources de courant parallèle tandis que g la conductance équivalente comme indiqué dans la figure ci-dessous
Laissez-je représenter le courant résultant des sources de courant parallèle tandis que g la conductance équivalente comme indiqué dans la figure ci-dessous


Ensuite, la source de courant résultante est convertie en une source de tension équivalente comme indiqué dans la figure ci-dessous
 Ainsi,
Ainsi,
Le signe positif (+) et négatif (-) semble inclure les cas où les sources peuvent ne pas fournir de courant dans la même direction.
Aussi,

Et comme nous le savons,
I = v / r, et nous pouvons également écrire r = i / g comme g = i / r
Ainsi, l’équation peut être écrite comme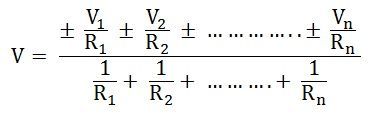
Où r est la résistance équivalente connectée à la source de tension équivalente en série.
Ainsi, l’équation finale devient

Étapes pour résoudre le théorème de Millman
Les étapes suivantes sont utilisées pour résoudre le réseau par le théorème de Millman
Étape 1 – Obtenir la conductance (g1G2,….) De chaque source de tension (V1V2,….).
Étape 2 – Trouvez la valeur de la conductance équivalente G en supprimant la charge du réseau.
Étape 3 – Maintenant, appliquez le théorème de Millman pour trouver la source de tension équivalente V par l’équation illustrée ci-dessous
Étape 4 – Déterminez la résistance de série équivalente (R) avec les sources de tension équivalentes (v) par l’équation
Étape 5 – Trouvez le actuel iL coulant dans le circuit à travers la résistance de charge RL par l’équation
