Théorème de compensation indique que dans un réseau linéaire invariant dans le temps lorsque la résistance (r) d’une branche non couplée, transportant un courant (i), est modifiée par (ΔR), les courants de toutes les branches changeraient et peuvent être obtenus en supposant que Une source de tension idéale de (VC) a été connecté de telle sorte que VC = I (Δr) en série avec (r + Δr) lorsque toutes les autres sources du réseau sont remplacées par leurs résistances internes.
Dans le théorème de la rémunération, la tension source (VC) s’oppose au courant d’origine. En termes simples, le théorème de compensation peut être indiqué comme – la résistance de tout réseau peut être remplacée par une source de tension, ayant la même tension que la chute de tension à travers la résistance qui est remplacée.
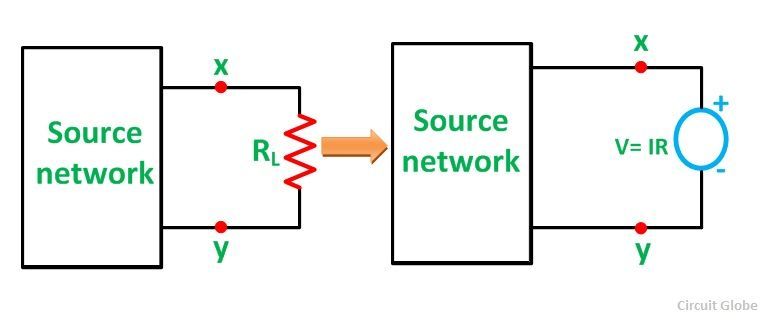 Explication
Explication
Assuons-nous une charge rL être connecté à un réseau source DC dont l’équivalent de Thevenin donne V0 Comme la tension du Thevenin et RÈME Comme la résistance de la Thevenin comme indiqué dans la figure ci-dessous:
 Ici,
Ici,

Que la résistance de charge soit modifiée en (RL + ΔRL). Étant donné que le reste du circuit reste inchangé, le réseau équivalent de Thevenin reste le même que celui indiqué dans le diagramme du circuit ci-dessous:
 Ici,
Ici,

Le changement de courant étant appelé Δi
Donc,

Mettre la valeur de i ‘et i à partir de l’équation (1) et (2) dans l’équation (3), nous obtiendrons l’équation suivante:

Maintenant, en mettant la valeur de I à partir de l’équation (1) dans l’équation (4), nous obtiendrons l’équation suivante:

Comme nous le savons, VC = I Δrl et est connu comme tension compensatrice.
Par conséquent, l’équation (5) devient,

Par conséquent, le théorème de la compensation indique qu’avec le changement de résistance à la branche, les courants de branche changent et que le changement est équivalent à une source de tension de compensation idéale en série avec la branche opposant le courant d’origine, où toutes les autres sources du réseau sont remplacées par leurs résistances internes .
