Qu’est-ce que la puissance de synchronisation et le coefficient de couple ?

Définition : – Puissance de synchronisation est défini comme la variation de la puissance synchrone P en fonction de la variation de l’angle de charge δ. On l’appelle aussi le Rigidité du couplage, Stabilité ou Facteur de rigidité. Il est représenté comme P._syn. Une machine synchrone, qu’il s’agisse d’un générateur ou d’un moteur, lorsqu’elle est synchronisée avec des jeux de barres infinis, a une tendance inhérente à rester en synchronisme.

Considérons un générateur asynchrone transférant une puissance constante P_un à un angle de charge constant δ₀. Supposons qu’en raison d’une perturbation transitoire, le rotor du générateur accélère, résultant d’une augmentation de l’angle de charge de dδ. Le point de fonctionnement de la machine passe à une nouvelle ligne de puissance constante et la charge sur la machine augmente jusqu’à P_un +δP. La puissance constante absorbée par la machine ne change pas et la charge supplémentaire qui s’ajoute diminue la vitesse de la machine et la ramène au synchronisme.

De même, en raison d’une perturbation transitoire, le rotor de la machine ralentit, ce qui entraîne une diminution de l’angle de charge. Le point de fonctionnement de la machine passe à une nouvelle ligne de puissance constante et la charge sur la machine diminue jusqu’à (P_un – δP). Puisque l’entrée reste inchangée, la réduction de la charge accélère le rotor. La machine arrive à nouveau en synchronisme.

L’efficacité de cette action corrective dépend de la modification du transfert de puissance pour un changement donné de l’angle de charge. La mesure de l’efficacité est donnée par Synchronisation Coefficient de puissance.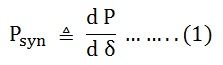

Puissance de sortie par phase du coefficient de couple de synchronisation du générateur à rotor cylindrique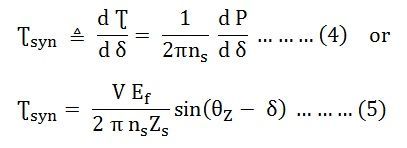

Dans de nombreuses machines synchrones Xs >> R. Par conséquent, pour une machine à rotor cylindrique, négliger les équations de saturation et de résistance statorique (3) et (5) devient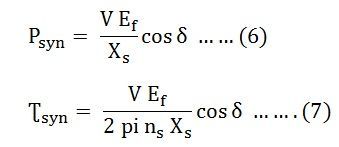

Pour une machine à pôles saillants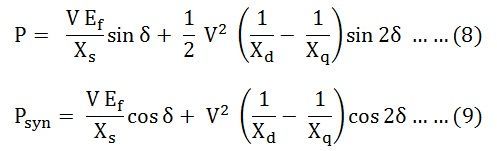

Unité de coefficient de puissance de synchronisation P_syn

Le coefficient de puissance de synchronisation est exprimée en watts par radian électrique.

Donc,

Puisque π radians = 180⁰

1 radian = 180/π degrés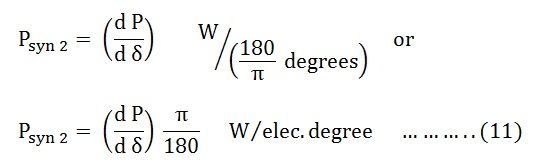

Si P est le nombre total de paire de pôles de la machine.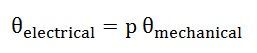

Le coefficient de puissance de synchronisation par radian mécanique est donné par l’équation ci-dessous :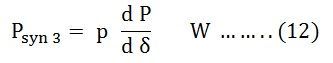

Le coefficient de puissance de synchronisation par degré mécanique est donné comme suit :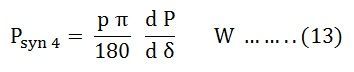

Coefficient de couple de synchronisation

Coefficient de couple de synchronisation donne lieu au coefficient de couple de synchronisation à vitesse synchrone. Autrement dit, le couple de synchronisation est le couple auquel la vitesse de synchronisation donne la puissance de synchronisation. Si Ʈ_syn est le coefficient de couple de synchronisation, alors l’équation est donnée comme suit : Où,

• m est le nombre de phases de la machine
• ω_s = 2 π n_s
• n_s est la vitesse synchrone en tour par seconde

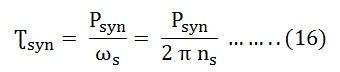
Importance du coefficient de puissance synchrone

Le Coefficient de puissance synchronetP_syn est la mesure de la rigidité entre le rotor et l’accouplement statorique. Une grande valeur de P_syn indique que l’accouplement est rigide ou rigide. Un accouplement trop rigide signifie que la machine sera soumise à des chocs, avec le changement de charge ou d’alimentation. Ces chocs peuvent endommager le rotor ou les bobinages. Nous avons,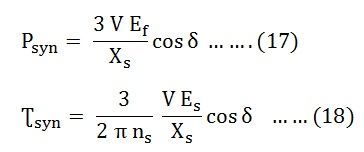

Les deux équations ci-dessus (17) et (18) montrent que P_syn est inversement proportionnelle à la réactance synchrone. Une machine avec de grands entrefers a une réactance relativement faible. La machine synchrone avec un entrefer plus grand est plus rigide qu’une machine avec un entrefer plus petit. Depuis P_syn est directement proportionnel à E_fune machine surexcitée est plus rigide qu’une machine sous-excitée.

L’action de restauration est importante lorsque δ = 0, c’est-à-dire sans charge. Lorsque la valeur de δ = ± 90⁰, l’action de restauration est nulle. Dans ces conditions, la machine est en équilibre instable et à une limite de stabilité en régime permanent. Par conséquent, il est impossible de faire fonctionner une machine à la limite de stabilité en régime permanent puisque sa capacité à résister à de petits changements est nulle à moins que la machine ne soit équipée d’un système d’excitation spécial à action rapide.