Le Méthode de deux wattmètres est expliqué, en prenant un exemple de charge équilibrée. En cela, nous devons prouver que la puissance mesurée par les deux wattmètres, c’est-à-dire que la somme des deux lectures de wattmètre est égale à la racine 3 fois de la tension de phase et de la tension de ligne (√3vLjeL Cosϕ) qui est la puissance réelle consommée dans une charge équilibrée en trois phases.
Le diagramme de connexion d’une charge équilibrée en trois phases connectée en tant que connexion d’étoile est illustré ci-dessous:
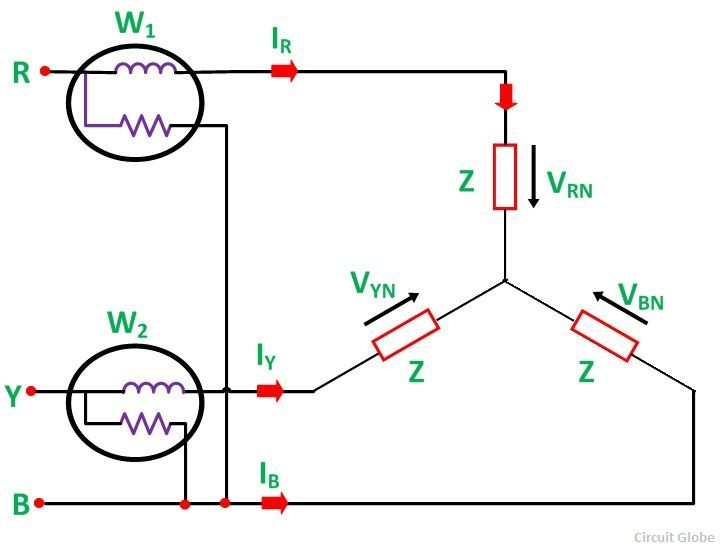
Contenu:
La charge est considérée comme une charge inductive, et donc, le diagramme de phaseur de la charge inductive est dessiné ci-dessous:
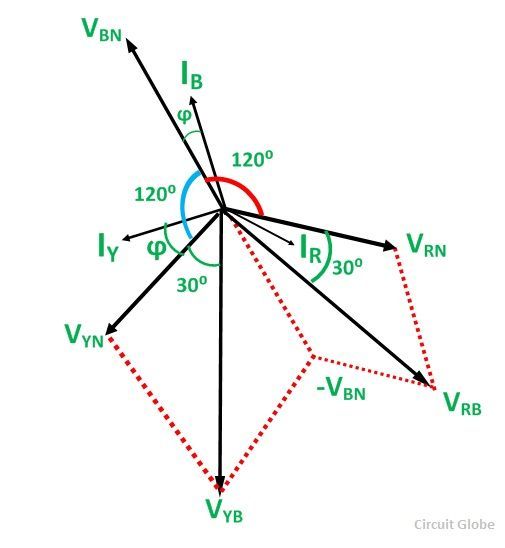 Les trois tensions VInfirmierVYn et VBNsont déplacés par un angle de 120 degrés électrique comme indiqué dans le diagramme de phaseur. Le courant de phase est en retard sur leurs tensions de phase respectives par un angle ϕ.
Les trois tensions VInfirmierVYn et VBNsont déplacés par un angle de 120 degrés électrique comme indiqué dans le diagramme de phaseur. Le courant de phase est en retard sur leurs tensions de phase respectives par un angle ϕ.
Maintenant, le courant traversant la bobine de courant du wattmètre, w1 sera donné comme:
![]()
La différence de potentiel à travers la pression ou la bobine potentielle du wattmètre, w1 sera:
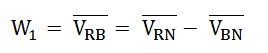
Pour obtenir la valeur de vYBinverser le phaseur VBN et ajoutez-le au phaseur VYn comme indiqué dans le diagramme du phaseur ci-dessus.
La différence de phase entre VRB Et moiR est (30⁰ – ϕ)
Par conséquent, la puissance mesurée par le wattmètre, w1 est:
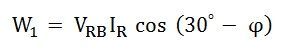
Courant à travers la bobine actuelle du wattmètre, w2 est donné comme:
![]()
La différence de potentiel à travers le wattmètre, w2 est
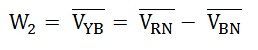
La différence de phase VYB Et moiY est (30⁰ + ϕ).
Par conséquent, la puissance mesurée par le wattmètre, w2 est donné par l’équation ci-dessous:
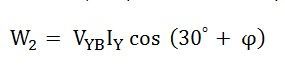
Depuis, la charge est dans un état équilibré, par conséquent,
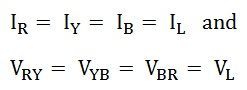
Par conséquent, les lectures du wattmètre seront:
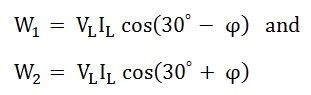
Maintenant, la somme de deux lectures de wattmètre sera donnée comme suit:
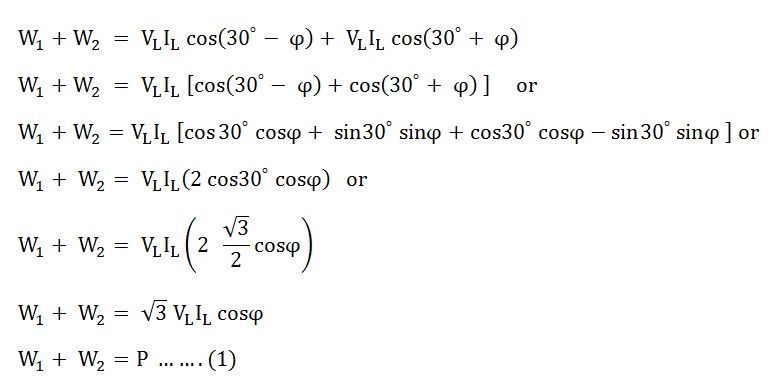 L’équation ci-dessus (1) donne la puissance totale absorbée par une charge équilibrée en trois phases.
L’équation ci-dessus (1) donne la puissance totale absorbée par une charge équilibrée en trois phases.
Ainsi, la somme des lectures des deux wattMètres est égale à la puissance absorbée dans une charge équilibrée en trois phases.
Détermination du facteur de puissance à partir des lectures de wattmètre
Comme nous le savons,
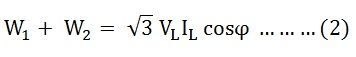
Maintenant,
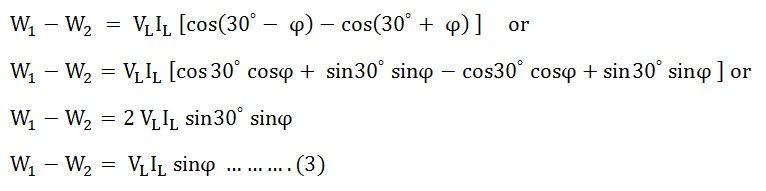 Diviser l’équation (3) par l’équation (2) nous obtenons,
Diviser l’équation (3) par l’équation (2) nous obtenons,
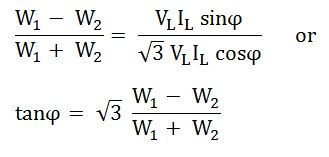
Le facteur de puissance de la charge est donné comme
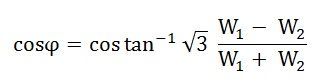
Détermination de la puissance réactive par deux méthodes WattMeter
Pour obtenir la puissance réactive, multipliez l’équation (3) par √3.
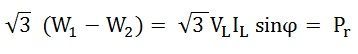
Par conséquent, une puissance réactive est donnée par l’équation ci-dessous:
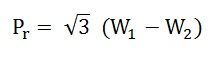 Pour la mesure de la puissance triphasée, vous pouvez également référer les deux sujets ci-dessous:
Pour la mesure de la puissance triphasée, vous pouvez également référer les deux sujets ci-dessous:
Voir également: Mesure de la puissance triphasée: trois méthodes de wattmètre
Voir également: Deux méthode de mesure de la puissance en wattmètre.
