Méthode d’admission est utilisé pour résoudre les circuits AC parallèles. L’admission montre la fiabilité du circuit électrique pour permettre au courant électrique de le traverser. Tout d’abord, nous devons connaître les significations de certains termes utilisés dans la méthode d’admission.
Admission
La réciproque de l’impédance d’un circuit AC est connue sous le nom d’admission du circuit. Étant donné que l’impédance est l’opposition totale offerte au flux de courant alternatif dans un circuit AC.
Par conséquent, l’admission est définie comme la capacité effective du circuit en raison de laquelle il permet au courant alternatif de le traverser. Il est représenté par (y). L’ancienne unité d’admission est MHO (Ʊ). Sa nouvelle unité est Siemens.
Le circuit a une impédance d’un ohm a l’admission d’un Siemens. L’ancienne unité était MHO.

Contenu:
- Admission
- Application de la méthode d’admission
- Étapes pour résoudre le circuit par méthode d’admission
- Triangle d’admission
- Conductance
- Sensibilité
Application de la méthode d’admission
Considérez le circuit à 3 branches illustré dans la figure ci-dessous. La conductance totale est trouvée en ajoutant simplement la conductance de trois branches. De même, la susceptation totale est trouvée en ajoutant algébriquement la susceptation individuelle de différentes branches.
 Conductance totale g = g1 + g2 + g3 +… ..
Conductance totale g = g1 + g2 + g3 +… ..
SUSCANTATION TOTALE B = (-B1) + (-b2) + b3….
Admission totale y = (g2 + B2)
Courant total i = vy; Facteur de puissance cosφ = g / y
Étapes pour résoudre le circuit par méthode d’admission
Considérez un circuit CA parallèle ayant une résistance et une capacité connectés en série et une résistance et une inductance également connectées en série comme indiqué sur la figure ci-dessous.
 Étape 1 – Dessinez le circuit selon le problème donné.
Étape 1 – Dessinez le circuit selon le problème donné.
Étape 2 – Trouvez l’impédance et l’angle de phase de chaque branche.

Étape 3 – Maintenant, trouvez la conductance, la sensibilité et l’admission de chaque branche.

Étape 4 – Trouvez la somme algébrique de la conductance et de la sensibilité.
![]()
Étape 5 – Trouvez l’admission totale (y) du circuit.
![]()
Étape 6 – Trouvez les différents courants de branche du circuit.

Étape 7 – Maintenant, trouvez le courant total I du circuit.
![]()
Étape 8 – Trouvez l’angle de phase de tout le circuit.

L’angle de phase sera à la traîne si B est négatif.
Étape 9 – Maintenant, trouvez le facteur de puissance du circuit.

Triangle d’admission
Triangle d’admission est également représenté de manière similaire au triangle d’impédance. Comme l’impédance (z) du circuit a deux composantes rectangulaires, la résistance (R) et la réactance (x). De même, l’admission (Y) a également deux composantes, la conductance (G) et la sensibilité (b).
Le triangle d’admission est illustré ci-dessous:
Conductance
La base du triangle d’admission est connue sous le nom de conductance, illustrée dans la figure ci-dessus.
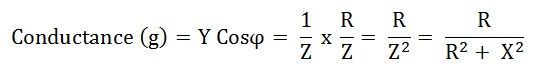 La valeur de la conductance est toujours positive indépendamment des paramètres du circuit.
La valeur de la conductance est toujours positive indépendamment des paramètres du circuit.
Sensibilité
La perpendiculaire du triangle d’admission est appelée sensibilité.
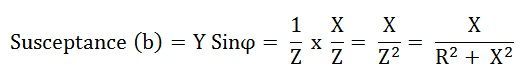 La sensibilité est positive pour la réactance capacitive comme le montre la figure ci-dessus (a) et est négative pour la réactance inductive comme le montre la figure (b).
La sensibilité est positive pour la réactance capacitive comme le montre la figure ci-dessus (a) et est négative pour la réactance inductive comme le montre la figure (b).

