Diagramme de cercle d’un moteur à induction

Le Schéma de cercle d’un moteur à induction est très utile pour étudier ses performances dans toutes les conditions de fonctionnement. La construction du diagramme du cercle est basée sur le circuit équivalent approximatif illustré ci-dessous. Il s’agit de la représentation schématique des performances du moteur d’induction. Le diagramme du cercle fournit des informations sur la puissance de sortie, les pertes et l’efficacité du moteur à induction.

Contenu:

• Construction du diagramme du cercle
• Résultat obtenu à partir du diagramme du cercle
• Signification des lignes sur le diagramme du cercle

Appliquer KCL (la loi actuelle de Kirchhoff)

Laissez la tension de phase V₁ être pris le long de l’axe vertical comme indiqué dans la figure ci-dessous:

Le Current sans charge I₀ = OA est en retard de V₁ par un angle ϕ₀. L’angle de facteur de puissance à vide ϕ₀ est de l’ordre de 60 à 80 degrés en raison du grand courant de magnétisation nécessaire pour produire le poteau de flux requis dans un circuit magnétique contenant les lacunes de l’air.

À la condition de non-charge, S = 0 et R₂/ sont infiniou nous pouvons dire que le r₂/ s est un circuit ouvert sans charge.

Ici, toutes les pertes de rotation sont considérées sous R₀ et la perte de co-charge est donnée par l’équation illustrée ci-dessous:

Le courant de rotor référé au stator est donné par:

Le courant i ‘₂ est à la traîne derrière la tension V₁ par l’angle d’impédance ϕ comme indiqué sur la figure ci-dessous:

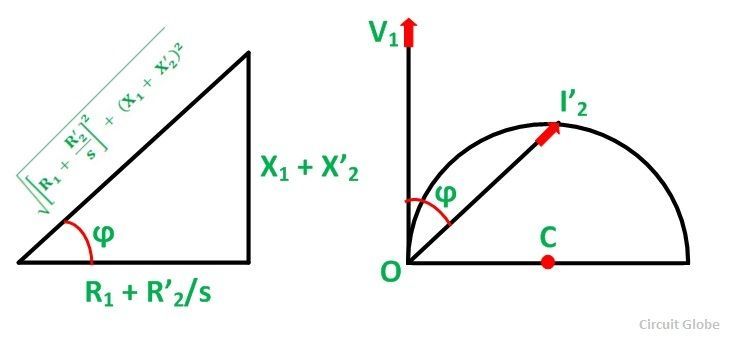
Où,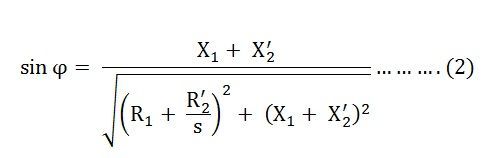

Combinant l’équation (1) et (2) nous obtenons

L’équation ci-dessus (3) est de la forme r = a sin φ qui représente un cercle sous forme polaire avec le diamètre a.

À partir de la figure ci-dessus (b), les points suivants sont illustrés.

• Le lieu de i ‘₂ est un cercle du diamètre v₁/ X₁ + X ‘₂
• Le rayon du cercle o’c = v₁/ 2 (x₁ + X ‘₂)
• Le centre C a les coordonnées (V₁/ 2 (x₁ + X ‘₂), 0)

Le diagramme de cercle résultant du moteur à induction est illustré ci-dessous:

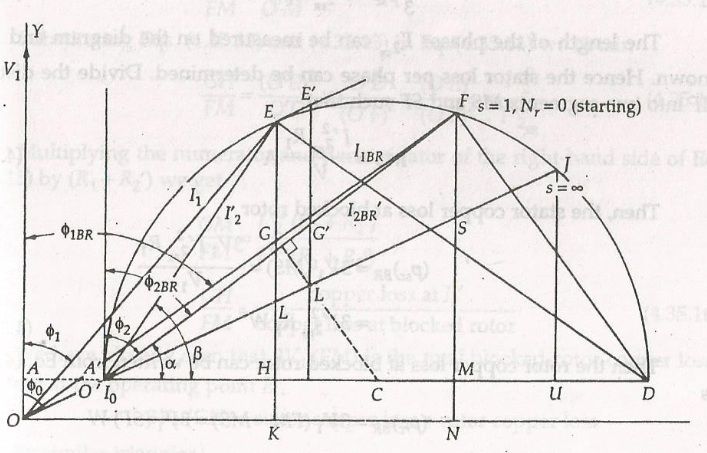
On voit que la pointe du phaseur I₁ coïncide avec celui du phaseur i ‘₂. Ainsi, le locus des deux₁ Et je₂ est le demi-cercle supérieur. je₁ Et je₂ rayon de l’origine o et o ‘respectivement. Quand le moteur est démarré S = 1 Avec la tension nominale, la pointe de i₁ Et je₂ sera à un moment donné F du cercle.

À mesure que le moteur s’accélère, les pointes de i₁ Et je₂ Déplacez-vous autour du cercle dans un sens anti-horaire. Ce processus se poursuit jusqu’à ce que le couple de sortie correspond au couple de charge. S’il n’y a pas de charge d’arbre, le moteur accélère à une vitesse synchrone. À ce point JE’₂ = 0 et je₁ = 0.

Construction du diagramme du cercle

Les données suivantes sont nécessaires pour construire le diagramme du cercle:

• Tension de phase du stator V₁ = V_L/ √3
• Current sans charge I₀
• Facteur de puissance sans charge Cosϕ₀
• Courant du rotor bloqué et facteur de puissance
• Résistance à la phase du stator r₁.

Étapes pour dessiner le diagramme du cercle d’un moteur à induction:

• Prenez la tension du phaseur V₁ le long de l’axe y.
• Choisissez un courant pratique. Avec o comme origine, tracez une ligne oo ‘= i₀ sous un angle ϕ₀ avec V₁.
• Tracer la ligne okn perpendiculaire à V₁. De même, tracez une ligne o’d perpendiculaire à V₁.
• Du point o tracez la ligne égale au courant du rotor bloqué i_1BR à la même échelle que je₀. Cette ligne est à la traîne en V₁ par l’angle du facteur de puissance du rotor bloqué ϕ_1BR.
• Rejoignez O’F et mesurez son ampleur dans les ampères. La ligne o’f représente i ‘_2BR.
• Du point F, tracez une ligne FMN parallèle à V₁. Cette ligne est perpendiculaire à O’D et sur.
• Calculer ms = i ‘²_2BRR₁/ V₁ et Locate Point S. Rejoignez les O et l’étend pour rencontrer le cercle à J.
• Dessinez la bissectrice perpendiculaire de l’accord O’F. Cette bissectrice passera à travers le centre du cercle au point C. Maintenant avec le rayon CD ‘ou CD dessinez le cercle.

Résultat obtenu à partir du diagramme du cercle

Supposons que le courant de ligne i₁ est connu. Avec le centre à O, dessinez un arc avec le rayon i₁. Cet arc coupe le cercle au point de fonctionnement E. tracez la ligne EK et localise le point H, L, G.

Les résultats suivants sont obtenus à partir du diagramme du cercle indiqué ci-dessus.

• Puissance d’entrée = 3v₁ Ke
• Pertes de rotation = 3v₁ Kh
• Stator Copper Perte = 3V₁ HL
• Perte de cuivre du rotor = 3V₁ LG
• Puissance de sortie = 3V₁ Ge
• Couple de sortie = 3V₁ LE / Ω_s
• Couple de départ = 3v₁ SF / Ω_s
• Glisser = lg / le
• Vitesse = ge / le x n_s
• Efficacité = GE / KE
• Facteur de puissance = KE / OE

Signification des lignes sur le diagramme du cercle

Ligne d’entrée sur

La distance verticale entre n’importe quel point du cercle et la ligne SUR représente la puissance d’entrée. Par conséquent, la ligne sur est appelée le ligne d’entrée.

Ligne de sortie O’F

La distance verticale entre n’importe quel point du cercle et la ligne O’g représente le puissance de sortie. Par conséquent, ligne DE est appelé le ligne de sortie.

Ligne électrique de l’espace aérien O’J

Ligne El représente la puissance de l’espace d’air p_g; doubler O’l est appelé le ligne d’alimentation de l’espace aérien. Depuis, Ʈ_d = P_g/ Ω_s. Cette ligne est également connue sous le nom Ligne de couple.