Dans Delta (Δ) ou connexion en maillagela borne finie d’un enroulement est connectée pour démarrer la borne de l’autre phase et ainsi de suite qui donne un circuit fermé. Les conducteurs à trois lignes sont exécutés à partir des trois jonctions du maillage appelé Conducteurs de ligne.
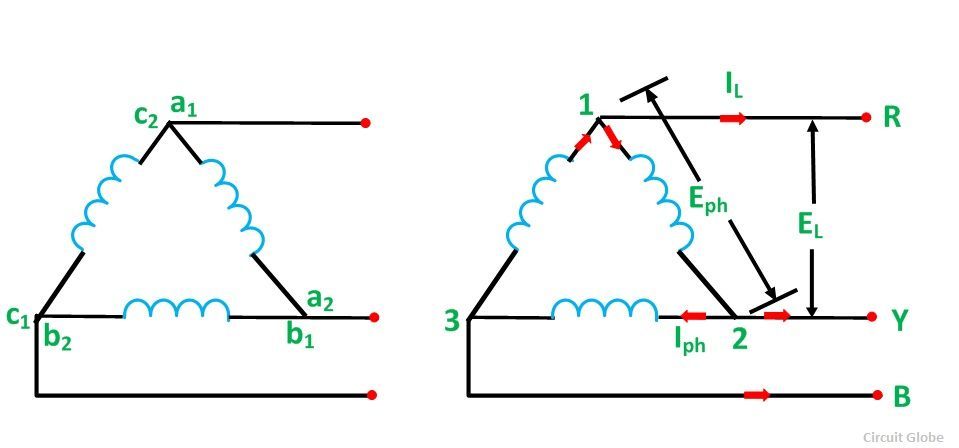
La connexion sous forme delta est indiquée dans la figure ci-dessous:
Contenu:
Pour obtenir le Connexions deltaun2 est connecté avec b1b2 est connecté avec c1 et c2 est connecté à un1 comme indiqué dans la figure ci-dessus. Les trois conducteurs R, Y et B fuient les trois jonctions connues sous le nom Conducteurs de ligne.
Le courant traversant chaque phase est appelé Courant de phase (IPH)et le courant circulant à travers chaque conducteur de ligne est appelé Courant de ligne (iL).
La tension à travers chaque phase est appelée Tension de phase (epH)et la tension à travers deux conducteurs de ligne est appelée Tension de ligne (eL).
Relation entre la tension de phase et la tension de ligne dans la connexion delta
Pour comprendre la relation entre la tension de phase et la tension de ligne dans la connexion delta, considérez la figure A illustrée ci-dessous:
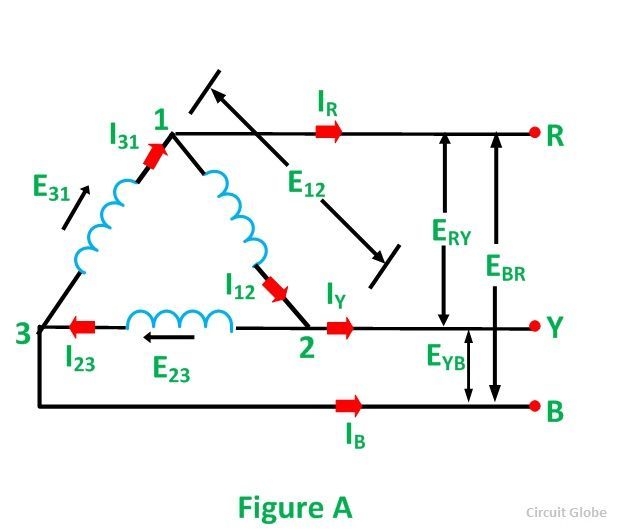 Il ressort clairement de la figure que la tension à travers les bornes 1 et 2 est la même que dans les bornes R et Y.
Il ressort clairement de la figure que la tension à travers les bornes 1 et 2 est la même que dans les bornes R et Y.
![]()
De la même manière,
![]()
: les tensions de phase sont
![]()
Les tensions de ligne sont:
![]()
Par conséquent, dans la tension de la ligne de connexion delta est égal à la tension de phase.
Relation entre le courant de phase et le courant de ligne dans la connexion delta
Comme dans le système équilibré, le courant triphasé I12JE23 Et moi31 sont égaux en amplitude mais sont déplacés les uns des autres par 120 ° électriques.
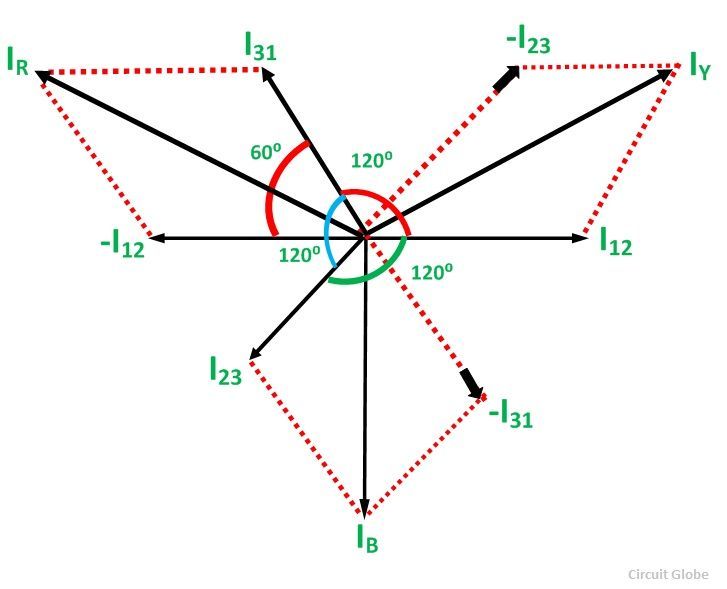
Le diagramme de phaseurs est montré ci-dessous:
 Ainsi,
Ainsi,
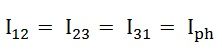
Si nous regardons la figure A, on voit que le courant est divisé à chaque jonction 1, 2 et 3.
Appliquer la loi de Kirchhoff à la jonction 1,
Les courants entrants sont égaux aux courants sortants.
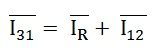
Et leur différence vectorielle sera donnée comme:
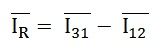
Le vecteur i12 est inversé et est ajouté dans le vecteur i31 Pour obtenir la somme vectorielle de i31 et –i12 comme indiqué ci-dessus dans le diagramme du phaseur. Donc,
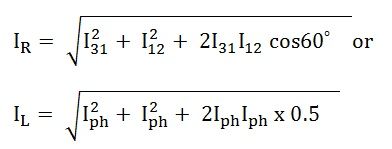
Comme nous le savons, jeR = ILdonc,
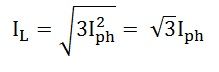
De la même manière,
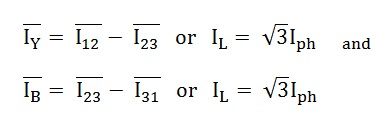
Par conséquent, dans la ligne de connexion delta, le courant est de la racine trois fois de courant de phase.
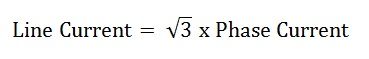
Il s’agit de la connexion Delta dans un système triphasé.
