Le circuit équivalent d’un Moteur à induction monophasé Peut être obtenu par deux méthodes nommées la théorie des champs et la théorie du champ croisé. Premièrement, le circuit équivalent est développé sur la base de la double théorie des champs tournante lorsque seul son enroulement principal est sous tension.
Considérant le boîtier lorsque le rotor est stationnaire et que seul l’enroulement principal est excité. Le moteur se comporte comme un transformateur monophasé avec son court-circuit secondaire. Le diagramme de circuit équivalent du moteur monophasé avec uniquement son enroulement principal énergisé est illustré ci-dessous:
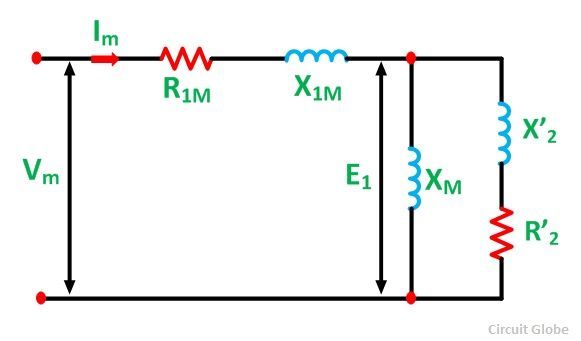
Ici,
- R1m est la résistance de l’enroulement du stator principal.
- X1m est la réactance des fuites de l’enroulement du stator principal.
- XM est la réactance magnétisante.
- R ‘2 La résistance au rotor de l’arrêt est-elle appelée l’enroulement du stator principal.
- X ‘2 est la réactance des fuites du rotor à l’arrêt est appelée l’enroulement du stator principal.
- Vm est la tension appliquée.
- jem est le principal courant d’enroulement.
La perte de base sera supposée être regroupée avec les pertes mécaniques et errantes dans le cadre des pertes de rotation du rotor. Le flux d’espace d’air pulsé dans le moteur à l’arrêt est résolu en deux flux égaux et opposés avec le moteur. L’impédance d’arrêt de chacun des rotors appelée l’enroulement du stator principal est donnée comme suit: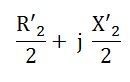
Le circuit équivalent d’un moteur à induction à enroulement unique à phase unique avec le rotor de l’arrêt est illustré ci-dessous. L’avant et le flux vers l’arrière induit une tension eMF et emb respectivement dans l’enroulement du stator principal. Em est la tension induite résultante dans l’enroulement principal.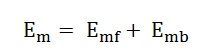
À la condition d’arrêt eMF = Emb
Maintenant, avec l’aide d’un enroulement auxiliaire, le moteur est démarré. Lorsque le moteur atteint sa vitesse normale, l’enroulement auxiliaire est retiré. La résistance efficace du rotor d’un moteur à induction dépend du glissement du rotor.
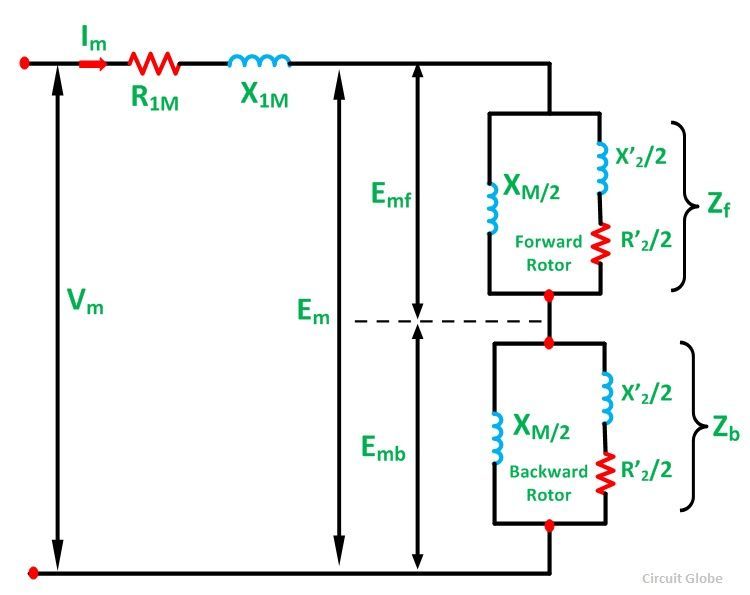
Dans le diagramme de circuit ci-dessus, la partie espace d’air est divisée en deux parties. La première partie montre l’effet du flux rotatif vers l’avant et la deuxième partie montre l’effet du flux rotatif vers l’arrière. La résistance efficace du rotor par rapport au flux rotatif vers l’avant est R‘2/ 2S et en ce qui concerne le flux rotatif vers l’arrière est r ‘2/ 2 (2 s).
Lorsque les glissements vers l’avant et vers l’arrière sont pris en compte, le circuit équivalent illustré ci-dessous est formé. Dans cet état, le moteur fonctionne seul sur l’enroulement principal.
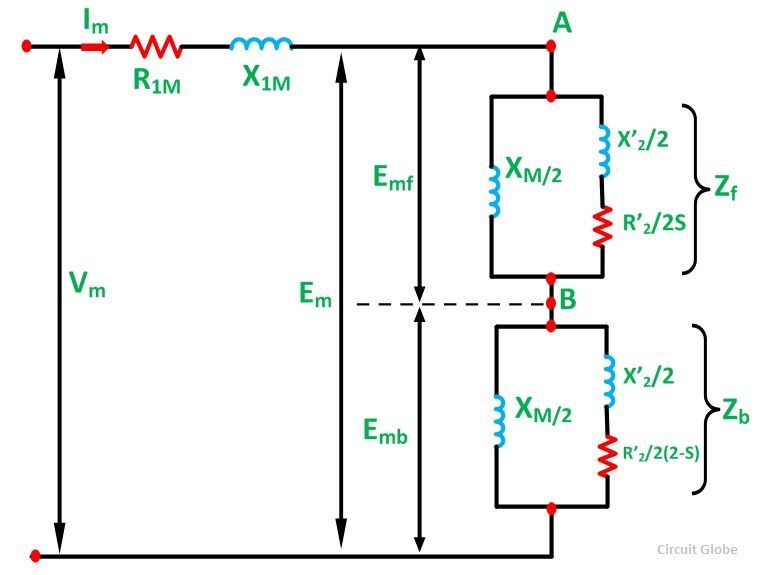
L’impédance du rotor représentant l’effet du champ avant référé à l’enroulement du stator m est donné par une impédance ci-dessous: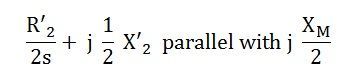
L’impédance du rotor d’un moteur à induction monophasé représentant l’effet du champ vers l’arrière référé à l’enroulement du stator m est donné par une impédance illustrée ci-dessous: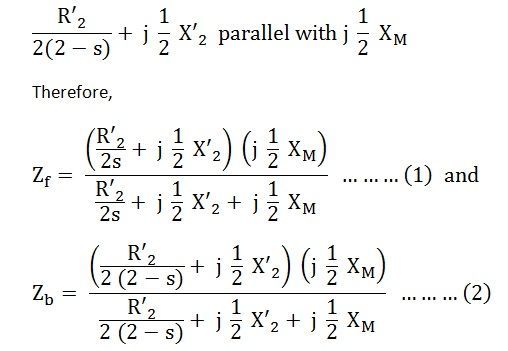
Le circuit équivalent simplifié d’un moteur à induction monophasé avec uniquement son enroulement principal énergisé est illustré dans la figure ci-dessous: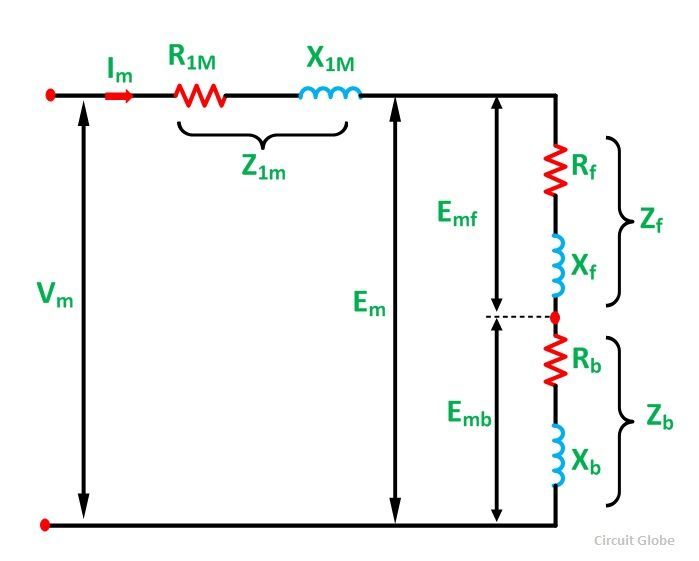
Ici,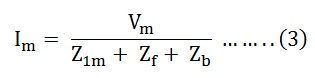
L’équation ci-dessus (3) est l’équation du courant dans l’enroulement du stator.
