Caractéristique de facteur de puissance zéro (ZPFC)

Caractéristique de facteur de puissance zéro (ZPFC) d’un générateur est une courbe de la tension de borne de l’armature et du courant de champ. La machine fonctionne avec un courant d’armature constamment noté à une vitesse synchrone et un facteur de puissance à décalage nul. La caractéristique du facteur de puissance zéro est également appelée Caractéristique potentielle.

Pour maintenir un facteur de puissance très faible, l’alternateur est chargé au moyen de réacteurs ou par un moteur synchrone excité. La forme de ZPFC ressemble beaucoup à celle de l’OCC

Le diagramme de phaseurs Correspondant à zéro facteur de puissance La retard est illustrée ci-dessous:

Dans le diagramme du phaseur illustré ci-dessus, la tension de borne V est considérée comme le phaseur de référence. À zéro facteur de puissance à la traîne, le courant d’armature I_un est en retard de V par 90 degrés. je_unR_un est tiré parallèle à i_un Et moi_unX_al perpendiculaire à je_un.

E_g est la tension générée par phase.

Le diagramme de phaseurs à ZPF à la traîne avec la résistance de l’armature R_un négligé est indiqué ci-dessous:

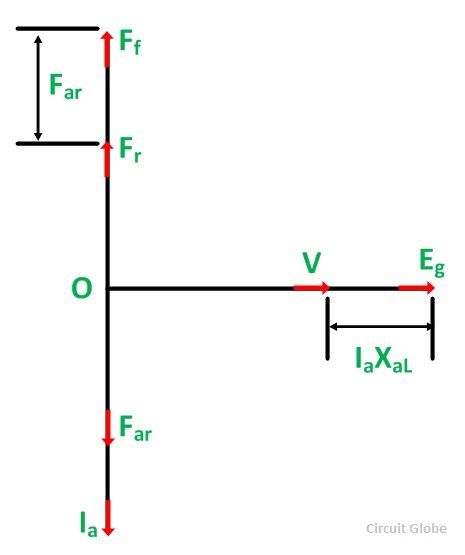Où,

• F_arde est la réaction d’armature MMF. Il est en phase avec le courant d’armature IA.
• F_f est le MMF de l’enroulement du champ principal (champ MMF de champ).
• F_r est le MMF résultant.

Le champ mmf f_f est obtenu en soustrayant f_arde de f_r de sorte que

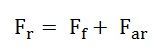À partir du diagramme de phaseur ci-dessus, on voit que la tension de borne V, la chute de tension de réactance I_unX_al, et la tension générée E_g tous sont en phase. Par conséquent, v est pratiquement égal à la différence arithmétique entre E_g Et moi_unX_al.

Le phasor FRIE MMF F_fF_r et f_arde sont en phase. Leurs amplitudes sont liées par l’équation ci-dessous:

Les deux équations ci-dessus, c’est-à-dire l’équation (1) et (2) constituent la base du triangle de poche.

Si l’équation (2) est divisée les deux côtés par t_fil est converti en sa forme de courant de champ équivalent. Ici t_f est le nombre effectif de tours par pôle sur le champ du rotor.

Donc,

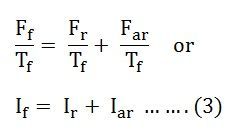À partir de l’équation ci-dessus, la somme du courant résultant et du courant de réaction d’armature donne le courant de champ.