Le système électrique est de deux types, à savoir le système monophasé et le système triphasé. Le système monophasé n’a qu’un seul fil de phase et un seul fil de retour, il est donc utilisé pour la transmission de faible puissance.
Le système triphasé comporte trois fils sous tension et un renvoie le chemin. Le système triphasé est utilisé pour transmettre une grande quantité d’énergie. Le Système triphasé est divisé principalement en deux types. L’un est un système triphasé équilibré et l’autre est un système triphasé déséquilibré.
Contenu:
Le système d’équilibre est un système dans lequel les charges sont réparties également dans les trois phases du système. L’amplitude de la tension reste la même dans les trois phases et est séparée par un angle de 120º.
Dans le système asymétrique, l’amplitude de la tension dans les trois phases devient différente.
Analyse du circuit triphasé équilibré
Il est toujours préférable de résoudre les circuits triphasés équilibrés en fonction de chaque phase. Lorsque la tension d’alimentation triphasée est donnée sans référence à la valeur de ligne ou de phase, alors c’est la tension de ligne qui est prise en compte.
Les étapes suivantes sont indiquées ci-dessous pour résoudre les circuits triphasés équilibrés.
Étape 1 – Tout d’abord, dessinez le schéma du circuit.
Étape 2 – Déterminer XLP =XL/phase = 2πfL.
Étape 3 – Déterminer XCP =XC/phase = 1/2πfC.
Étape 4 – Déterminer XP. = X/phase = XL –XC
Étape 5 – Déterminer ZP. = Z/phase = √R2P. +X2P.
Étape 6 – Déterminer cosϕ = RP./ZP.; le facteur de puissance est en retard lorsque XLP >XCP et il est en tête quand XCP >XLP.
Étape 7 – Déterminez la phase V.
Pour connexion étoile VP. = VL/√3 et pour connexion triangle VP. = VL
Étape 8 – Déterminer que jeP. = VP./ZP..
Étape 9 – Maintenant, déterminez le courant de ligne IL.
Pour la connexion en étoile, jeL = jeP. et pour la connexion delta, jeL = √3 jeP.
Étape 10 – Déterminez la puissance Active, Réactive et Apparente.
Analyse d’un circuit triphasé déséquilibré
L’analyse du système triphasé déséquilibré est légèrement difficile et la charge est connectée soit en étoile, soit en triangle. Le sujet est abordé en détail dans l’article intitulé Conversion d’étoile en delta et de delta en étoile.
Interconnexion du système triphasé
Dans un générateur CA triphasé, il y a trois enroulements. Chaque enroulement possède deux bornes (début et fin). Si une charge distincte est connectée à chaque enroulement de phase comme indiqué dans la figure ci-dessous, alors chaque phase alimente en tant que charge indépendante via une paire de fils. Ainsi, six fils seront nécessaires pour connecter la charge à un générateur. Cela rendra l’ensemble du système compliqué et coûteux.
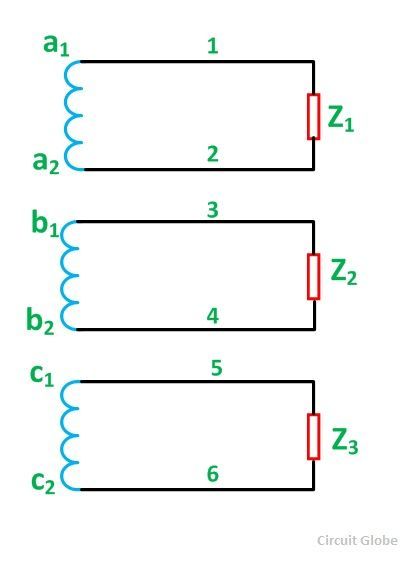
Par conséquent, afin de réduire le nombre de conducteurs de ligne, les enroulements triphasés d’un générateur AC sont interconnectés. L’interconnexion des enroulements d’un système triphasé peut se faire des deux manières suivantes :
Connexion étoile ou étoile (Y) Voir aussi : Connexion en étoile dans un système triphasé
Connexion maillée ou Delta (Δ). Voir aussi: Connexion Delta dans un système triphasé
Connexion de charges triphasées dans un système triphasé
L’alimentation triphasée étant connectée en étoile et en triangle. De même, les charges triphasées sont également connectées soit en connexion étoile, soit en connexion Delta. La charge triphasée connectée en étoile est représentée dans la figure ci-dessous :
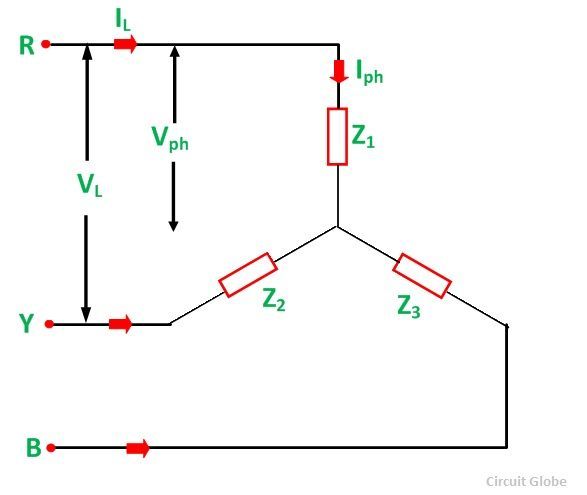La connexion en triangle des charges triphasées est illustrée dans la figure ci-dessous :
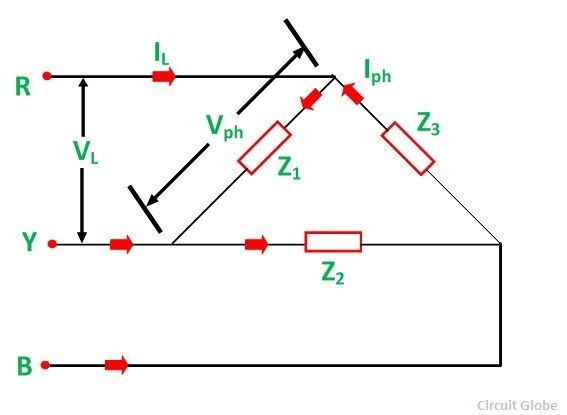Les charges triphasées peuvent être équilibrées ou déséquilibrées comme indiqué ci-dessus. Si les trois charges Z1,Z2 et Z3 ont la même amplitude et le même angle de phase, alors la charge triphasée est dite être une charge équilibrée. Dans de telles connexions, tous les courants de phase ou de ligne et toutes les tensions de phase ou de ligne sont de même amplitude.